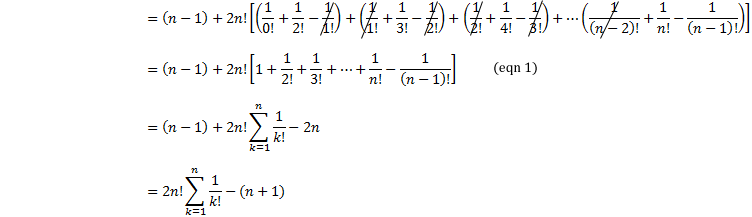This post is actually a comment on following post
http://pramnegi.blogspot.com/2009/11/dons-permutaion.html
Following is the first among the many algorithms to find permutations, that are stated in Knuth's “Art of computer programming volume 4 fascicle 2”.
Knuth gives the credit to narayana pandit of 14th century for the following algorithm and mark it as “algorithm L”.
This algorithm find the lexicographically sorted permutation.
For the first time read the algorithm without explanations inside ( ).
Intuition
Now, off course this algorithm works but in order to get intuition behind this algorithm, we need to run the whole algorithm for a particular case.
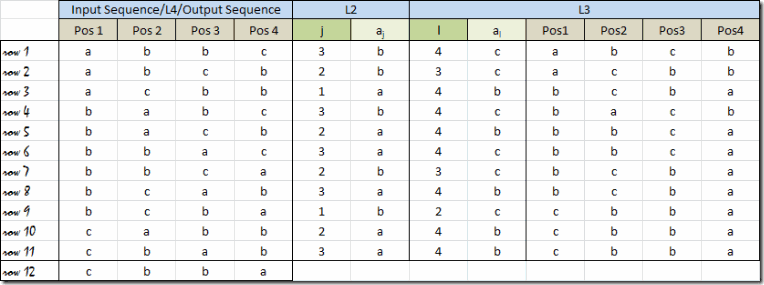
Let us run this for set {a, b, c, d}
Table 1
Ok, now see the Pos 1 only of all the rows.
first we place all the permutations starting from a (row 1 to 6),
then from b (row 7 to 12),
then from c (row 13-18) and
then d (19-24).
Now for all rows with a on Pos 1, see the Pos 2.
Again we first place all the permutations with b at Pos 2 (row 1-2),
then with c (row 3-4) and
then with d (row 5-6).
It is as expected as we are generating permutations in lexicographic increasing order.
Now let us try to answer a question:
Q: If we look at only permutations that start with a (a at Pos 1), then given a particular permutation among it (say at row x), how can we be sure of that it is last such permutation. i.e., there are no more permutations that start with a and comes after row x?
In the example above, row 6 is the last such row that there are no more rows after it that starts with a. So, if we are at row 6, how do we know that if there do not exist any more permutation that starts with a and come after row 6?
A: Answer is simple. Following are the rows with a on Pos 1
Now if leave the first column, then we see all the permutation of b, c and d in lexicographic increasing order.
Since, We know in the list of permutations of b, c and d (lexicographically sorted), last permutation will be (d,c, b), therefore, the permutation at row 6 (a,d,c,b) will be the last such permutation with a on Pos 1.
Since at this row, we are done with all permutations with a on Pos 1, we consider the next element on Pos 1 i.e., b[1]
we will discuss this point soon.
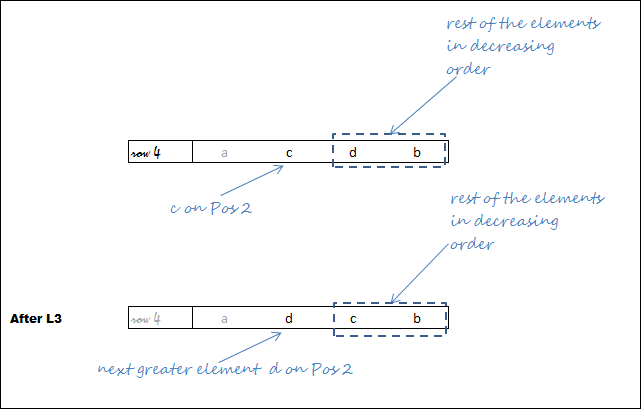
So far we have established the meaning of L2. Let us take one more case, to understand L2.
Consider row 3 and 4:
Now both rows are starting with (a,c).
So being at row 4 we see that rest of the elements i.e., b and d are in decreasing order i.e., (d, b).
so now we know that with c on Pos 2 (and a on Pos 1), we are done with all the permutations and it is time to try next larger element on Pos 2 i.e., d[2]
Now, read back the Knuth's explanation of L2.
Hope, now it makes sense.
Coming to L3, read “[1]” again (and the context in which it was written). So how do we now find next greater element on Pos 1?
We know that the rest of elements that follow are in decreasing order. Since we have to find an element just greater than a (element on Pos 1), we can start or search from end and go up to Pos 2. Any time we get an element greater than a, we stop our search. Here we find b at Pos 4, so our next element to be placed at Pos 1 is b. so we swap a with b.
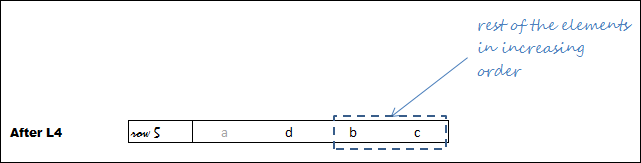
With now b being on Pos 1, for the elements that follow Pos 1, we have to start with first permutation in lexicographically increasing order of the rest of elements.
Now the rest of the elements at following positions are already in decreasing order (remember L2), so we just have to reverse their sequence (which is step L4).
Let us take another example for L3, Read “[2]” again (and the context in which it was written). So, now our task is to find out next greater element on Pos 2.
we start looking from the last for the element which is just greater than c (element on Pos 2).
Pos 4 b is not greater, leave it.
Pos 3 d is greater, ok so we found it.
so d is the element now to be placed at Pos 2. we swap c with d. We now get
For the elements that follow Pos 2, we have to start with first permutation in increasing order, so we just reverse the sequence following Pos 2 (step L4).
Now, read back the Knuth's explanation of L3
So, aj has now become greater than al, this is obvious as we have replaced the element at Pos j with element just greater than itself (found at Pos l)
Hope, now it makes sense too.
Knuth summarizes these steps as follows:
Till now we have seen working of algorithm L on case where elements are not repeated.
But this algorithm works on multi-set too. Let us see, why it do not cause problem with that.
Let us run the algorithm for multi-set {a, b, b, c}
Table 2
Let us see the step L3 again. We find the element just greater than the element on Pos j. Note "greater than" and not "greater than equal to". Had it been, the latter case, then we would have got repeated permutations. (24 instead of 12). When we are at row 4 and we have to find the next element for Pos 2, we do not consider the b at Pos 4 (because it is equal to element at Pos 2 and not greater than it) and just skip to c at Pos 3.
Knitting this all together, process of gaining intuition for algorithm is complete.
Complexity
We will first determine the total no. of comparisons required in step L2 and length of sequence to be reversed in step L4.
Now note that if for finding aj in step 2, we reach at Pos 1 i.e., j=1, then in that case, at next step we will change element at Pos 1 (i.e., it means we are done with cases with current element at Pos 1). Starting from second last position, for reaching up to Pos 1, we need 3 comparisons.
Also,
We know from table 1 that element at Pos 1 is changed 3 times.
For j=1, length of the sequence to be reversed is 3.
So, we have the following information so far
Now take the case in which, we reach at Pos 2 in step 2 i.e., j=2. At next step, we will change element at Pos 2 while keeping the element at Pos 1 same.
From table 1, we know that element at Pos 2 is changed 2 times for a fixed element at Pos 1. Also, 4 different elements take the place at Pos 1 equal no. of times. So, total no. of times the element at Pos 2 is changed is 4*2.
Also, starting from second last position, for reaching up to Pos 2, we need 2 comparisons (Same is also the sequence length to be reversed in L4).
Now, let us update the table
Consider the case, where we reach at Pos 3 in step L2 i.e., j=3. At next step, we will change element at Pos 3 while keeping the elements at Pos 1 and Pos 2 same. Keeping up with the logic we have previously applied, we have
Add to it, the case of last permutation where j is not found in L2 but anyways 3 comparisons were made before that. Also, there is nothing to be reversed.
Now,
For n=4,
Similarly, if you find the same for n=5, you will get
For n=5,
Now, let us try to generalize,
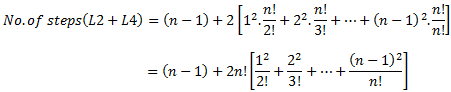
Now, let us attempt to find the total no. of comparisons required in step L3.
No. of comparisons in L3 depends upon value of j found in L2.
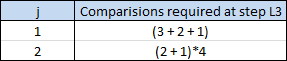
For j=1, there is an equal chance of l being 2, 3 or 4 (no. of comparisons required being 3, 2 and 1 respectively)
For j=2 and a fixed element at Pos 1, there is an equal chance of l being 3 or 4 (No. of comparisons required between 2 and 1 respectively). Also, 4 different elements take the place at Pos 1. So we have,
For j=3 and fixed elements at Pos 1 and Pos 2, there could be only 1 possible value of l i.e., l=4. However 4 different elements take the place at Pos 1 and at each of these 4 times, remaining 3 different elements takes the place at Pos 2. So, we have
Last entry is added to the table above corresponding to the case of last permutation, where we decided to terminate the algorithm at step L2 itself.
Now, for n=4,
Generalizing, we get
we have already solved for the first term. See “eqn 1”
Now,
So, it is safe to specify the bounds on running time as O(n!) and it is the best possible as total no. of outputs in this case is n!
One cannot expect anything lower than that.
So far we have found the complexity for the case when algorithm is applied on sets (all elements are distinct). But as soon as we move to the case of multi-set, things become too complicated. I can’t handle the mathematics for that so looking for support.
Program
Following is the algorithm implemented in C++. It works on containers supporting both forward and reverse iterators and both input and output iterators.
Following are some examples of how to use the permute function:
Example 1
Example 2
Example 3